Rough Notes on ResNets and Neural ODEs
1. ResNets
ResNets are short for Residual Networks, a type of neural network building block that incorporates the identity function, in the form of: \(\mathbf{y} = \mathbf{x} + f(\mathbf{x}, W)\)
1.1 References Used
- Deep Residual Learning for Image Recognition
- Identity Mappings in Deep Residual Networks
- An Overview of ResNet and its Variants
- Understanding and Implementing Architectures of ResNet and ResNeXt for state-of-the-art Image Classification
1.2 Summary
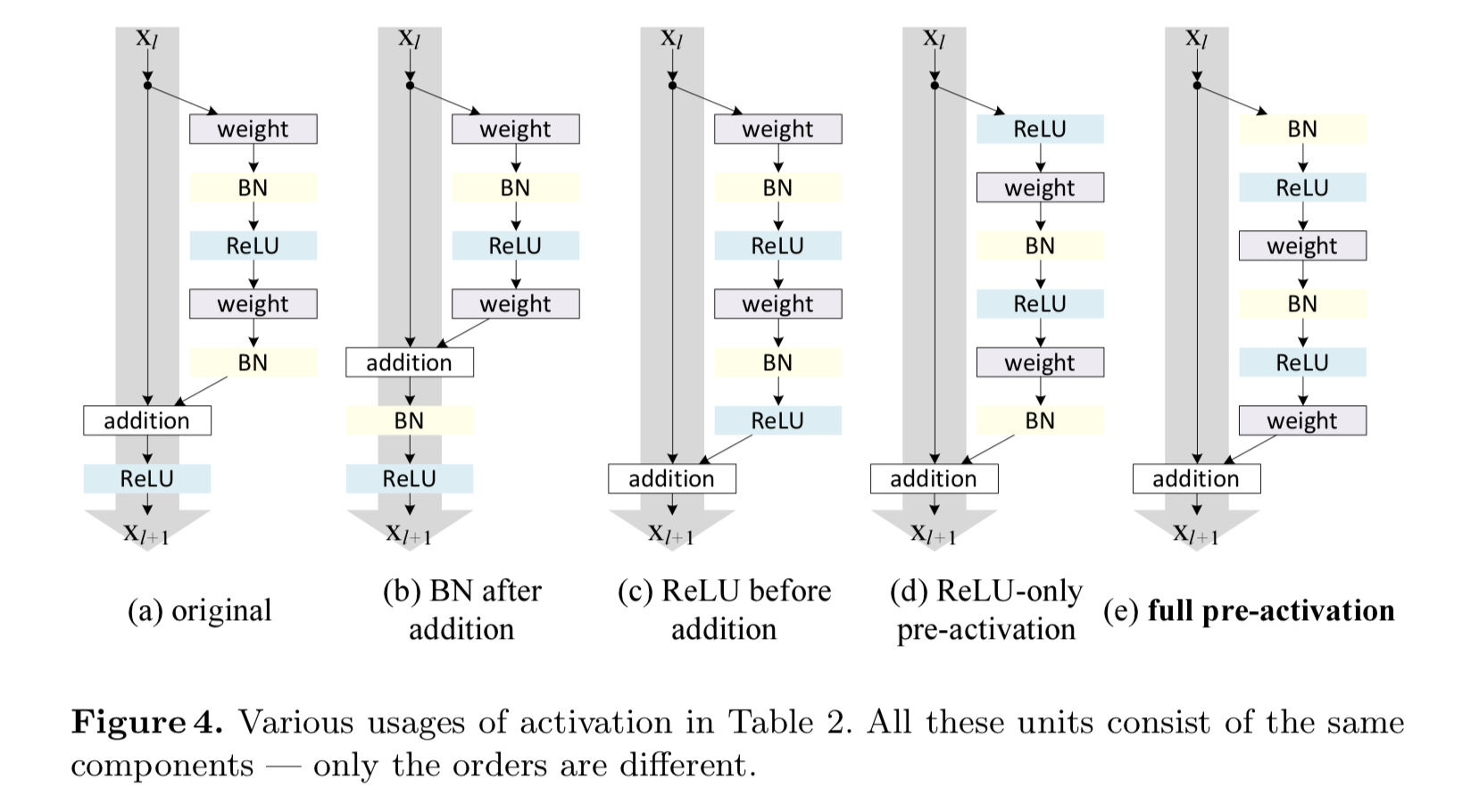
- Deep neural networks have problems with gradients approaching zero, but adding many ResNet blocks does not decrease accuracy (as much)
- As seen in the figure above, newer ResNet architectures improve upon the original ResNet by preserving the potential for an identity function between different ResNet blocks, while the original pushed its output through an activation function (ReLU)
- ReLU before preactivation (c) restricted each ResNet block to a non-negative residual, and had worse performance, so ReLU needed to be conducted before the weights
- Moving the Batch Normalization (BN) step resulted in (e) having the best performance
- Batch Normalization is when each dimension of an input into a hidden layer is standardized by calculating its mean and variance for the whole mini-batch
- BN implementations incorporate two more learnable parameters after the normalization step, for each dimension \(k\), where \(\mathbf{y}^{k} = \gamma^{k} \mathbf{x}^{k} +\beta^{k}\)
- Both ResNet architectures showed a drastic improvement on ImageNet and CIFAR tasks
1.3 Extensions
- ResNet in ResNet is a generalization of the original ResNet, and incorporates two "streams" of information in a single block:
- Residual Stream allows the identity function to be used and the residual to be learned
- Transient Stream allows learning of a traditional non-linear function and unnecessary information to be discarded easily
- Neural ODEs (as seen below) are a continuous generalization of ResNets
2. Neural ODEs
Neural Ordinary Differential Equations (ODEs), also known as ODE-Nets, are a way to combine ODE solvers with neural network architectures. This can happen in a few ways: incorporate neural networks into dynamical system/differential equation research, incorporate ODEs into neural network architectures
2.1 References Used
This is the Hacker News discussion on the Neural ODE paper, with David Duvenaud replying to some questions himself.
And finally, this is the PyTorch implementation with examples.
2.2 Summary
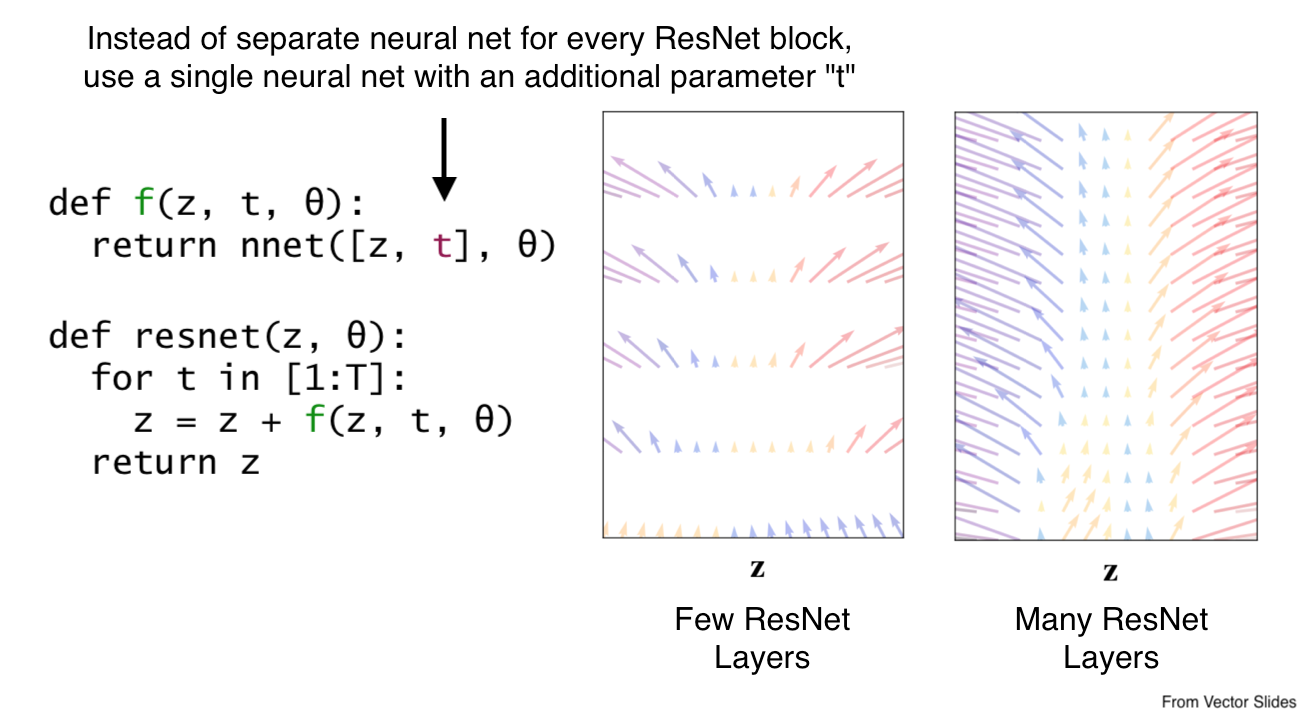
- ResNets are very similar to an Euler method, a method for solving ODE (differential equations with respect to one independent variable, usually time)
- Euler method starts with an initial value, and then adds the derivative at each subsequent time multiplied by the time step
- ResNets start with the input (initial value), and add a residual at each layer
- If we model each layer in the ResNet as a unit time step in the Euler method, i.e. \(h=1\), the residual function is equivalent to the derivative with respect to time.
- We want to increase the granularity of the time steps/hidden states, and make the residual function continuous
- Problem: This means the number of layers and parameters approaches infinity!
- Solution: Create a single neural net that accepts current time as an input, and make this the new derivative function for the ODE solver
- Backpropogation uses the "Adjoint Sensitivity Method", and there is an understandable proof of the gradients with regards to the neural network parameters \((\theta)\), as well as the initial and finish times \((t_0,t_1)\), in the appendix of the ArXiv paper
- The gradients for a Neural ODE block within a larger architecture, for example a classifier, can still be calculated (backprop)
2.3 Benefits
- Much fewer parameters required to achieve the same performance for classification tasks
- Much less memory is required for training with regards to depth: \(\mathcal{O}(1)\)
- Neural ODEs incorporate powerful ODE solvers that allow a fine tradeoff between speed and accuracy
- For example, after training with high accuracy, the test data may be processed instead with high speed
- This paper allows neural networks to be efficiently used in dynamical systems research, and also ODE solvers in deep neural network architectures
2.4 Time Series Analysis
- Neural ODEs have a well defined latent state at any evaluation time, which is in contrast with Recurrent Neural Networks (RNNs)
- A trick used for incorporating irregular time intervals in RNNs include passing the time delta, but Neural ODEs perform much better than RNNs on some tasks
- Neural ODEs for time series are trained using a Variational Auto-encoder (VAE) architecture
- Although not mentioned in the paper, the talk by David Duvenaud mentions that the RNN for the encoder has been replaced (or augmented? not sure ...) by running the dynamics of the ODE solver backwards. This needs further investigation
- Time-series Neural ODEs also allows for the modeling of the observations as well as the time of observation
- Non-homogenous Poisson 🐟 Processes are a more general form of Poission Processes, with a varying rate \(\lambda(\cdot)\) over time
- The likelihood of the Non-homogenous Poisson process can be determined with a rate function \(\lambda(\mathbf{z}(t))\) that is simultaneously learned by the Neural ODE
2.6 Continuous Normalizing Flows
- Currently in progress ...
- What are Normalizing Flows?
- What is FFJORD?